GEOMETRIE ANALYTIQUE

page d'accueil>>Mathématiques>>géométrie>>>géométrie analytique

Encore une fois, il est bon de commencer par un rappel, il s'agit cette fois de l'équation cartésienne KESAKO??? nan, j'exagère vous devez tous en avoir plus ou moins des souvenirs (pas tous agréables je vous l'accorde) de ce type d'équation, mais voici quand même un petit rappel qui ne fera de mal à personne => au mieux, c'est un élargissement de la définition que vous connaissiez avant la première S.

Une équation cartésienne d'une figure F est une relation vérifiée par tous les points de la figure F et seulement par ces points

On ne peut être plus claire => le livre n'est parfois pas si mal!!!

I- Équation cartésienne dans le plan

1) Équation d'une droite dans le plan

Soit (O;i;j) un repère du plan:
soit a, b et c trois réels tels que a et b ne soient pas tous les deux nuls.

L'équation ax + by + c = 0 est l'équation cartésienne de la droite D, dont un vecteur directeur a pour coordonnées u (-b;a)

Une droite n'admet qu'une seule équation réduite de la forme y = mx + p où m et p sont deux réels. Mais ça vous le saviez déjà..., ça n'est pas nouveau (pas vraiment!!!)

2) Vecteur normal a une droite

Soit une droite D (oh comme c'est original!!!),
Un vecteur n est normal à D veut dire que n est orthogonal à tous les vecteurs directeurs de la droite D.

Dans un repère orthormal, si n(a, b) est un vecteur donné, alors toute droites de vecteur normal n a pour équation cartésienne: ax + by + c = 0.

3) Équation de cercle

=> Si le cercle est défini par son centre et son rayon:

Soit (O;i;j) un repère orthonormal du plan:,
R est un réel strictement positif et ω un point de coordonnées (a;b).

Tout point M (x;y) appartient au cercle de centre ω et de rayon R si et uniquement si ωM = R, ce qui se traduite lors d'une démonstration par la relation
=> (x-a)² + (y-b)² = R².

=> Si le cercle est défini par son diamètre:

Soit [AB] un diamètre du cercle,
comme vous l'avez tous vu en troisième, que si le point M appartient au cercle de diamètre [AB] alors le triangle ABM est rectangle en M, avec les propriétés du produit scalaire de deux vecteurs orthogonaux, cela se traduit par la relation suivante:
M apparient au cercle de diamètre [AB] uniquement si AM.BM = 0.

II- Équation cartésienne dans l'espace

Encore un petit rappel sur comment calculer la distance entre un point A et un point B de l'espace
AB = -/ (x_B - x_A)² + (y_B - y_A)² + z_B - z_A)²

1) Sphère de centre O

On travaille toujours dans un repère orthonormal mais cette fois on y rentre un paramètre supplémentaire que l'on appelle la côte et qui est en fait l'axe z, "la troisième dimension" donc le repère est: (O;i;j;k) c'est la lettre k qui "représente" cet axe z.

Donc soit (O;i;j;k) un repère orthonormal de l'espace,
et R un réel strictement positif qui va représenter le rayon de la sphère (et non plus cercle faites!!! on est dans l'espace)

Alors une équation de la sphère est : x² + y² + z² = R²

2) Plan parallèles à un plan de coordonnées

Tout plan parallèle au plan qui a pour coordonnées (xOy) (perpendiculaire à l'axe (Oz)) admet une équation cartésienne de la forme z = α avec α réel
Tout plan parallèle au plan qui a pour coordonnées (xOz) (perpendiculaire à l'axe (Oy)) admet une équation cartésienne de la forme y = β avec β réel
Tout plan parallèle au plan qui a pour coordonnées (yOx) (perpendiculaire à l'axe (Ox)) admet une équation cartésienne de la forme x = ε avec ε réel

3) Cylindre de récolution

Il y a trois cas de figure qui s'offre à nous..., mais en tout les cas, R est un réel donné qui ne peut être que positif car il est le rayon du cylindre

Si l'axe des côtes est l'axe de révolution du cylindre, alors celui-ci a pour équation x² + y² = R².
Si l'axe des abscisses est l'axe de révolution du cylindre, alors celui-ci a pour équation y² + z² = R².
Si l'axe des ordonnées est l'axe de révolution du cylindre, alors celui-ci a pour équation x² + z² = R².

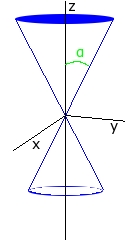
4) Cône de révolution

Il y a encore trois cas de figure qui s'offre à nous et R reste un réel donné qui ne peut être que positif car il est le rayon du cône

Si l'axe de révolution du cône de sommet O est l'axe des côtes, alors ce cône a pour équation x² + y² - βz² avec &beta = tan α (voir schéma ci-contre).
Si l'axe de révolution du cône de sommet O est l'axe des abscisses, alors ce cône a pour équation y² + z² - βx².
Si l'axe de révolution du cône de sommet O est l'axe des ordonnées, alors ce cône a pour équation x² + z² - βy².

Ainsi s'achève ce chapitre... j'éspère que pour vous tout a été le plus claire possible ou en tout cas, que j'ai pu vous apporter mes (très) modestes lumières sur le sujet...

bilan et exercices guidés